Diese Seite funktioniert nur mit Javascript.
Modell von Bertrand4.2.2.5 Kartelle und GefangegendilemmaAllgemeine Gleichgewichtstheorie
ieser Abschnitt behandelt die Analyse eines Duopolproblems durchgängig an einem Zahlenbeispiel. Den Ausgangspunkt des Zahlenbeispiels bildet die Kartelllösung. Allerdings präsentiert der Beitrag nicht die Ergebnisse der etablierten (klassischen) Duopolmodelle nach Cournot, von Stackelberg und Bertrand, sondern zeigt einen Lösungsansatz mithilfe einfacher spieltheoretischer Überlegungen auf. Die Lösungen des Zahlenbeispiels der klassischen Modelle finden sich am Ende dieses Abschnitts.
Preis
(EUR/Reifen) |
Absatzmenge
(Stückzahl) |
100
|
3.000.000
|
110
|
2.800.000
|
120
|
2.600.000
|
130
|
2.400.000
|
140
|
2.200.000
|
150
|
2.000.000
|
160
|
1.800.000
|
170
|
1.600.000
|
180
|
1.400.000
|
190
|
1.200.000
|
200
|
1.000.000
|
210
|
800.000
|
220
|
600.000
|
1. Die Ausgangssituation
Für das Zahlenbeispiel, das die Grundlage dieses Beitrages bildet, sei ein Markt durch die folgenden Annahmen beschrieben: Zwei Unternehmen, Zonti und Purelli, teilen sich in einem Land den Reifenmarkt. Die Unternehmen sind in allen Aspekten vergleichbar: Umsatz, Beschäftigung, Produktionsverfahren. Mit Reifen fertigen sie ein relativ homogenes Standardprodukt, bei dem es keine wesentlichen Qualitätsunterschiede gibt. Konkurrenz aus dem Ausland haben die Unternehmen nicht zu befürchten, da ein hoher Importzoll auf Reifen erhoben wird, der den Markt für ausländische Wettbewerber unattraktiv macht. Ein Markteintritt potenzieller inländischer Konkurrenten ist mittelfristig nicht zu erwarten.
Zonti hat die Unternehmensberatung UB beauftragt, die Produktion und den inländischen Reifenmarkt zu analysieren und strategische Empfehlungen auszusprechen. Die wesentlichen Ergebnisse der UB-Studie sind in den Tabellen 1 und 2 wiedergegeben. Tabelle 1 gibt Auskunft über den insgesamt zu erwartenden Reifenabsatz bei alternativen Preisen. Dabei hat UB unterstellt, dass beide Anbieter etwa gleiche Preise für ihr Produkt fordern, weil dies in der Vergangenheit regelmäßig zu beobachten war und infolge der Ähnlichkeit der Produkte auch für die Zukunft zu erwarten ist. Der hervorgehobene Wert kennzeichnet die aktuell beobachtete Situation. Bei den anderen Werten handelt es sich um Einschätzungen der Unternehmensberatung. Bei steigenden Preisen rechnet UB dem Gesetz der Nachfrage entsprechend mit sinkendem Absatz.
Bezugsgröße
|
Berechnung
|
Wert [EUR]
|
(1) Stückkosten
|
(1)
|
150
|
(2) Preis
|
(2)
|
200
|
(3) Produktion
|
(3)
|
500.000
|
(4) Werbung
|
(4)
|
0
|
(5) Absatz
|
(5)
|
500.000
|
(6) Umsatz
|
(6) = (5)*(2)
|
100.000.000
|
(7) Kosten
|
(7) = (3)*(1)+(4)
|
75.000.000
|
(8) Stückgewinn
|
(8) = (2)-(1)
|
50
|
(9) Gewinn
|
(9) = (6)-(7)
= (8)*(5) |
25.000.000
|
Geschäftsbereich "Reifen"
Die Angaben in Tabelle 2 beziehen sich auf die Situation im Zonti-Reifenwerk. Die jährliche Produktion beträgt eine halbe Million Reifen, d.h. Zonti hält einen Marktanteil von 50 Prozent. Aus den weiteren Angaben folgt, dass bei einem Stückgewinn von 50 Euro je Reifen der Profit im Geschäftsbereich Reifen 25 Mio. Euro beträgt. Ein weiteres Ergebnis der Analyse von UB, das aus der Tabelle nicht hervorgeht, bezieht sich auf die Produktionskosten. Es wird vermutet, dass selbst bei stärkeren Veränderungen der Produktionsmenge die Stückkosten mit 150 Euro pro Reifen nahezu konstant bleiben. Da sich die Analyse auf langfristige, strategische Überlegungen bezieht, wird nicht zwischen fixen und variablen Kosten unterschieden.
Unter den alternativen Marktstrategien, die UB vorgeschlagen hat, findet eine besondere Aufmerksamkeit im Vorstand von Zonti: Es sei von der Hypothese auszugehen, dass eine aggressive Werbekampagne für Zonti-Reifen den Absatz auf dem Markt insgesamt etwas vergrößern würde und sich zugleich die Marktanteile deutlich zugunsten von Zonti verschöben. Konkret wird angenommen, dass man mit einem Werbebudget von 10 Mio. Euro vom derzeitigen Marktvolumen noch 25 Prozent hinzugewänne. Der Zuwachs im Marktvolumen, den Zonti voll für sich verbuchen könnte, wird auf 100.000 Reifen geschätzt.
Eine Analyse der momentanen Situation würde übrigens zeigen, dass beide Duopolisten stillschweigend ein Kartell bilden und sich den Monopolgewinn in Höhe von 50 Mio. Euro teilen. (Die Preis-Absatz-Funktion für die Daten in Tab. 1 lautet $p = 250 -0,05x$ mit $x$ als Reifen in 1000 Stück; die Kosten sinf mit der Funktion $K= 150x$ berechnet.)
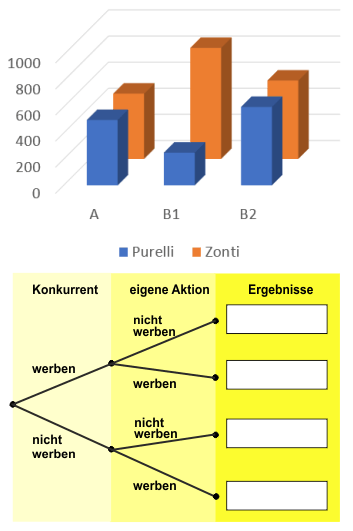
2. Analyse der Werbe-Strategie
Kommen wir zurück auf den Vorschlag der Unternehmensberatung UB. Um die Auswirkungen eines entsprechenden Verhaltens möglichst einfach analysieren zu können, seien die Annahmen noch etwas verschärft: Erstens seien die beiden Unternehmen absolut spiegelbildlich. Während Zonti also UB beauftragt hat, hat Purelli gleichfalls eine Unternehmensberatung beauftragt und stellt seinerseits Strategieüberlegungen an. Zweitens sei noch angenommen, der Absatz auf dem Markt würde sich um 20 Prozent steigern lassen, wenn beide Unternehmen eine Werbekampagne mit einem jeweiligen Volumen von 10 Mio. Euro starten würden. Die Absatzsteigerung würde entsprechend geringer ausfallen, würde nur ein Unternehmen werben. Die Steigerung im Marktvolumen käme jeweils voll dem Werbetreibenden zugute. Außerdem sei unterstellt, dass die Unternehmen keine gemischten Strategien wählen, also nicht Werbung und Wettbewerb über den Preis zugleich betreiben.
Stellen wir uns eine Besprechung bei Zonti vor, in der die Unternehmensberatung UB ihr Konzept erörtert. UB hat dazu ein Flipchart wie in Abb. 1 vorbereitet. Strategie A im oberen Diagramm zeigt den Status quo. Strategie B1 zeigt die Marktanteile der beiden Unternehmen, wenn nur Zonti wirbt: Das Marktvolumen steigt auf 1,1 Mio. Stück, der Marktanteil verschiebt sich zugunsten von Zonti: es werden 75 Prozent des Ausgangsvolumens plus 100 Tsd. Reifen Zuwachs gewonnen, so dass der Absatz von 500 auf insgesamt 850 Tsd. Reifen steigen würde. Würde auch Purelli werben (B2), rechnen die Marktforscher mit einem gesamten Absatz von 1,2 Mio. Reifen, der sich zu gleichen Teilen auf Zonti und Purelli verteilt. Eine Situation haben die Marktforscher nicht dargestellt: dass nur der Konkurrent wirbt. In diesem Fall würde das spiegelbildliche Ergebnis zur Strategie B1 eintreten.
Zonti*
|
|||
| nicht werben | werben
|
||
| Purelli | nicht werben | 25
|
32,5
|
25
|
12,5
|
||
| werben | 12,5
|
20
|
|
32,5
|
20
|
||
| * Grau hinterlegte Felder zeigen den Gewinn von Purelli. | |||
Duopolisten bei alternativer
Strategiewahl (Auszahlungsmatrix)*
Wie wirken sich die beiden Strategien "Werben" (B) und "Nicht-Werben" (A) auf die Gewinnsituation von Zonti aus? Nach wie vor können wir mit einem Stückgewinn von 50 Euro je Reifen kalkulieren, müssen allerdings die 10 Mio. Euro Kosten der Werbekampagne bei Strategie B in Rechnung stellen. Da beide Unternehmen sich nur entscheiden können, zu werben oder es bleiben zu lassen, sind vier unterschiedliche Konstellationen denkbar, die in Tab. 3 dargestellt sind.
Nun kann bei Zonti eine Entscheidung getroffen werden: Angenommen, Purelli würde nicht werben, dann wäre die optimale Entscheidung, selbst zu werben, da in diesem Fall der Gewinn auf 32,5 Mio. Euro steigen würde (= 50 Euro/Reifen bei 850 Tsd. Reifen abzgl. 10 Mio. für die Werbekampagne). Angenommen, Purelli würde werben, dann wäre die optimale Entscheidung, ebenfalls zu werben, da sonst die ungünstigste Situation überhaupt mit nur 12,5 Mio. Euro Gewinn einträte. Bei Werbung wären es aber immerhin 20 Mio. Euro. Damit steht fest: Egal was der Konkurrent tut, die bessere Entscheidung heißt immer "Werbung".
Aus Sicht von Purelli stellt sich die Situation aber genau spiegelbildlich dar. Also wählt auch Purelli die Werbestrategie, so dass für beide Unternehmen der Gewinn jeweils 20 Mio. beträgt. Obwohl aus beider Sicht dies die jeweils optimale individuelle Entscheidung darstellt, ist sie für beide gemeinsam dennoch suboptimal. Sie würden besser fahren, wenn sie wie bisher auf Werbung verzichten würden. Diese Situation heißt Gefangenendilemma (prisoner's dilemma). Sie ist durchaus vergleichbar mit der klassischen Cournot-Lösung des Duopolproblems: keiner von beiden kann seine Situation verbessern, wenn nicht der andere seine Strategie ändert (ein sog. Nash-Gleichgewicht). Würden andererseits beide offen oder stillschweigend übereinkommen, nicht zu werben, so bestünde für jeden ein großer Anreiz, von der Übereinkunft abzuweichen, da sich das Betrügen des "Vertragspartners" offensichtlich lohnt.
Das Ergebnis der Analyse der Werbeentscheidung hat jedoch wenig Überzeugungskraft, wenn man es an eigenen Beobachtungen tagtäglichen Marktgeschehens misst (z.B. der Beobachtung der Kraftstoffpreise). Die beiden Teilnehmer am Werbespiel überblicken die Situation und es ist von daher wenig wahrscheinlich, dass sie sich in der schlechtesten der denkbaren Lösungen verfangen. Warum sollten sie sich Jahr für Jahr mit 20 Mio. zufrieden geben, wenn sie 25 erreichen könnten? Würde sich an der Analyse also etwas ändern, wenn wir die beiden Konkurrenten die Entscheidungen über mehrere Jahre wiederholt treffen lassen?
2. Wiederholte Spiele
Bei einem fortgesetzten Spiel könnte uns folgende Überlegung helfen: hält sich einer der beiden Konkurrenten nicht an die getroffene Vereinbarung, auf Werbung zu verzichten - betrügt er also den anderen -, dann läuft er Gefahr, in den folgenden Perioden selbst Opfer von Werbung des Konkurrenten zu werden. Dauert das Spiel länger als nur eine Periode, dann besteht die Möglichkeit der Bestrafung. Es gibt dann also einen Anreiz, sich an die getroffene Vereinbarung zu halten. Nehmen wir konkret an, es werde 10 Perioden gespielt und zwar von Periode zu Periode das durch die Auszahlungsmatrix in Tabelle 3 beschriebene Spiel.
Stellen wir uns vor, es lägen bereits neun Perioden hinter uns. Das Spiel wird noch genau einmal gespielt, nämlich in der zehnten Periode. Dann haben wir wieder das einperiodige Spiel, das wir bereits analysiert haben. Hier kann die optimale Strategie für beide nur "Werbung" lauten. Das bedeutet aber, dass jeder Spieler weiß, dass er den Konkurrenten für Fehlverhalten in der letzten Periode nicht mehr bestrafen kann und sein eigenes Fehlverhalten in dieser Periode natürlich auch keine Strafe mehr nach sich zieht. Wenn der Spieler aber weiß, dass er in der letzten Periode auf jeden Fall hintergangen wird, dann ist es vernünftig, den Konkurrenten bereits in der vorletzten Periode zu betrügen. Diese Überlegung ist ihm aber ebenfalls bekannt, so dass es letztlich wiederum rational ist, gleich in der ersten Periode zu werben. Der Gedanke des fortgesetzten Spiels mit einer Bestrafungsmöglichkeit führt also (bei einem endlichen Spiel) auch nicht weiter.
Wie entsteht dann aber Kooperation? Zur Beantwortung dieser Frage hatte der Spieltheoretiker Axelrod (The evolution of cooperation, New York, 1984) eine pfiffige Idee. Wenn man das Problem analytisch nicht in den Griff bekommt, so bietet sich die Simulation an. Axelrod hat daraufhin Computerturniere veranstaltet, bei denen die Teilnehmer Strategien für das oben beschriebene Spiel eines Gefangenendilemmas einreichen konnten (im Prinzip genau dieses Spiel, nur mit anderen Werten). Von Periode zu Periode galt es für die Programme, jeweils nur die - übertragen auf das vorliegende Problem - Entscheidung "Werbung: ja oder nein" zu treffen. Dabei war den Programmen in jeder Spielrunde bekannt, wie der bisherige Spielverlauf aussah. Ein ganz simples Programm in Pseudocode hätte etwa wie folgt aussehen können:
start
wenn (periode div 2 == 0) dann "werbe" sonst "werbe nicht";
stop;
Dieses Programm wählt den Spielzug "werbe" in jeder geraden Perioden und wirbt nicht in jeder ungeraden Spielperiode, was natürlich eine recht primitive Strategie wäre. Ein zweites Beispiel für ein etwas komplexeres Programm wäre
start
wenn (periode=1) dann "werbe nicht"
sonst
wenn (gegner[periode-1] == "werbe") dann "werbe" sonst "werbe nicht";
stop;
Diese Strategie spielt "Wie Du mir, so ich Dir". Hat der Konkurrent in der Vorperiode geworben, dann wird mit Werbung gekontert, hat er sich wohlverhalten, dann wird das durch eigenes Wohlverhalten belohnt.
Axelrod hat die gesammelten Strategien gegeneinander spielen lassen und dabei einen evolutorischen Prozess simuliert, indem er Runde für Runde Strategien mit schlechten Ergebnissen hat ausscheiden lassen. Die Strategien haben also einen "Überlebenskampf" geführt, in dem die guten auch in der nächsten Runde dabei waren und die schlechten "ausgestorben" sind. Kritisch zu Axelrods Simulation lässt sich anmerken, dass eine einmal gewählte Strategie beibehalten werden muss, wohingegen Spieler in der Realität natürlich die Möglichkeit haben, während des Spiels zwischen Strategien zu springen.
Die Ergebnisse einer solchen Simulation sind nicht eindeutig. Sie hängen von der Parameterkonstellation und von den mitspielenden Strategien ab. Es ist also durchaus möglich, dass eine Strategie sich im Wettbewerb mit zehn anderen als die beste herausstellt, aber wenn sie nur gegen neun von den ursprünglichen zehn Gegnern antreten würde, nur den zweiten oder dritten Platz belegte oder noch schlechter abschnitte. Dennoch konnte Axelrod Eigenschaften von jenen Strategien identifizieren, die in den Simulationen mit hoher Regelmäßigkeit zu den "Überlebenden" zählten. Die vier Eigenschaften lauten, wenn man sie als Verhaltensregel formuliert
- 1. Vergelte beides.
- 2. Betrüge nie als Erster.
- 3. Sei nicht neidisch.
- 4. Sei nicht zu raffiniert.
Alle vier Regeln besitzen intuitiv einsichtige Erklärungen. Die erste Regel gibt den Hinweis, dass man Wohlverhalten des Gegenspielers belohnen, Fehlverhalten aber bestrafen soll ('reciprocity'). Man muss sich provozieren lassen. Würde man Fehlverhalten einfach "durchgehen" lassen, also immer kooperativ sein, liefe man Gefahr, ausgenutzt zu werden. Verhält sich der Gegenspieler aber wohl, so wird ihm durch eigenes Wohlverhalten signalisiert, dass dies ein vernünftiger Weg ist.
Dass man nicht als erster unkooperativ sein ('niceness') soll, ist recht plausibel. Man stelle sich nur vor, gleich in der ersten Runde begänne man das Spiel mit einem Betrugsmanöver. Das würde Vertrauen beim Gegenspieler zerstören und es wäre wahrscheinlich recht schwierig, wieder den kooperativen Weg einzuschlagen.
Auch sollte es gelingen, wenn man einmal vom gewinnbringenden kooperativen Weg abgekommen ist - wozu ja wegen der lockenden kurzfristigen Gewinnaussichten eine große Versuchung gegeben ist - wieder auf den langfristig lohnenden Pfad der Kooperation zurückzukehren. Dazu muss man dem Gegenspieler aber "Friedensangebote" unterbreiten, Kooperationsbereitschaft signalisieren, ihm sein Fehlverhalten nachsehen ('forgiveness/niceness'). Man wählt also die kooperative Strategie. Zieht der Gegenspieler mit, dann hat es sich gelohnt, weil wieder Aussicht auf langfristige Kooperation besteht. Andernfalls müsste man davon natürlich wieder Abstand nehmen.
Die letzte Regel ist vielleicht intuitiv nicht ganz so plausibel wie die ersten drei. Die Erklärung, warum es sich lohnt, eher unkompliziert zu sein ('clarity'), liegt darin, dass der Gegenspieler das eigene Verhaltensmuster schnell erkennen und begreifen kann, wenn man einfach und durchschaubar ist. Dadurch wird auch Vertrauen aufgebaut. Der Gegenspieler muss bei einer unkomplizierten Strategie nicht damit rechnen, unverhofft betrogen zu werden. Das bedeutet aber, dass auch ihm kein Anlass gegeben wird, von der kooperativen Strategie abzuweichen.
Eine Regel, die alle vier Bedingungen exzellent erfüllt, ist das bereits im Pseudocode vorgestellte Verhaltensmuster "Wie Du mir, so ich Dir" ("tit for tat"). Tatsächlich hat diese einfache Strategie Axelrods Turnier auch gewonnen (eine einzige beste Strategie gibt es - wie erwähnt - nicht, weil das Ergebnis des evolutorischen Prozesses auch von den Mitspielern abhängig ist; so könnte man das Ergebnis eines solchen Turniers dadurch manipulieren, dass man sich mit zwei Strategien beteiligt, bei der sich eine Strategie von der anderen ganz bewusst ausbeuten lässt und gegenüber Dritten grundsätzlich unkooperativ ist; wie in einem Wettrennen, in dem ein Läufer andere bewusst behindert, um einem Kameraden einen Vorteil zu verschaffen). Ausschlaggebend für den Erfolg von "tit for tat" ist nicht etwa, dass diese Strategie andere "schlägt". Ganz im Gegenteil: sie verliert gegen die meisten anderen im direkten Vergleich (z.B. gegen die sehr simple Strategie "betrüge immer"). Aber sie verliert nie hoch, denn sie lässt sich nicht ausbeuten. Wer mit ihr zusammentrifft, fährt selbst nur gut, wenn er kooperiert.
So lässt sich der Erfolg von "tit for tat" zusammenfassend etwa wie folgt beschreiben: Es lohnt sich nicht, in jedem direkten Vergleich der beste zu sein. Der erkämpfte Sieg kostet unter Umständen soviel Kraft, dass Dritte leicht vorbeiziehen. Viele gute Ergebnisse sind auf Dauer besser als wenige sehr gute bei zahlreichen schlechten. Und wenn man sich fragt, wie es denn in anderen Lebensbereichen, z.B. zwischenmenschlichen Beziehungen, mit Verhaltensmustern aussieht - so verkehrt scheint "tit for tat" auch dort nicht zu sein, oder?!
